ما هي الأعداد الكلية؟

ما هي الأعداد الكلية، ما هي الأعداد الصحيحة؟ غالبًا ما يختلف طلابنا في الأرقام ، ولا يعرفون الفرق بين مجموعات الأرقام المختلفة ، لذلك سنتعرف على ما هي الأعداد الصحيحة؟ ما الفرق بينه وبين مجموعات الأرقام الأخرى، وقد زادت التساؤلات حول هذا الموضوع، فهذا الموضوع من المواضيع المهمة التي تستغرق الكثير من الوقت لفهمها وتحليلها وما يؤدي إليها، فتابعونا خلال الأسطر القادمة من المقالة للتعرف على مزيد من المعلومات التي تتعلق بهذا الأمر.

تاريخ الدلالات رياضيا

حرص الإنسان منذ القدم على استخدام الأساليب الحسابية لفهم البيئة المحيطة به ، وبالتالي كان بحاجة إلى أرقام ، وقد ذكر المؤرخون أن الإنسان القديم لم يستخدم الأرقام ، بل استخدم الأصابع والحصى والعصي للعد وإجراء العمليات الحسابية:

تطورت الحضارات ، وتوسعت المفاهيم والعلم ، واختُرع العداد في الحضارة البابلية القديمة ، كطريقة معتمدة للعد. ظهرت رموز الأرقام في الحضارة المصرية القديمة ، ولكن ليس كل الأرقام.
على سبيل المثال ، في الحضارة المصرية القديمة ، تم تمثيل الرقم 1000 برمز زهرة اللوتس ، ورمز مقياس النيل للرقم 100 ، وما إلى ذلك ، وكانت الأرقام تُقرأ من اليمين إلى اليسار ومن أعلى إلى أسفل.
طور اليونانيون نظام الأرقام المصري وجعلوه أكثر سهولة ، باستخدام الأحرف اليونانية بدلاً من الرموز المصرية ، بحيث تم التعبير عن جميع الأرقام تقريبًا برموز أقل.
عبّر الإغريق عن الأرقام من 2-9 ، والأرقام 20-30-40 إلى 90 ، والأرقام 200-300-400 إلى 900 ، ولكل منها رمز أو رمزان على الأكثر.
كان نظام الأرقام هذا أسهل من النظام المصري. على سبيل المثال ، للتعبير عن الرقم 87 في النظام المصري ، تحتاج إلى حوالي 15 رمزًا ، بينما في النظام اليوناني تحتاج فقط إلى 3 رموز ، ورمزان للعد 7 ورمز واحد لعد 80.
بعد ذلك طور علماء المسلمين الأرقام ، وذلك بفضل العالم المسلم الخوارزمي لاختراعه الرقم صفر بعد أن اعتبر الإغريق والرومان أنه لا يوجد شيء مثل الرقم صفر وأن هذا شكل من أشكال الجنون والبدعة وحتى الكفر كذلك.

تجهيز الأرقام الكلية

كما ذكرنا أن رموز الأرقام لم تبدأ في الظهور إلا في الحضارة المصرية القديمة ، واستخدم المصريون القدماء رموزًا من بيئتهم المحيطة للتعبير عن الأرقام ، مثل القوس للرقم 10 ، وزهرة اللوتس للرقم 100 ، والضفدع لرقم 10000 ، وهكذا :

طور اليونانيون هذه الرموز وعبروا عن الأرقام بالأحرف الأبجدية ، مما سهل عملية العد والتعبير عن الأرقام. على سبيل المثال ، يمثل الحرف X الرقم 10 ويمثل الحرف V الرقم 5.
أما العرب فقد استخدموا الأرقام الهندية 0-1-2-3 وهكذا ، ورغم أنهم أرقام هندية إلا أنهم أطلقوا عليها اسم العربية لأن العرب كانوا أول من قدمهم للعالم وأوروبا والغرب. العالمية.
الأرقام الإنجليزية الحالية 0 – 1 – 2 – 3 هي الأرقام العربية التي استخدمها واخترعها العرب.
مع تطور اللغات ، تطورت الأعداد وظهرت رموز مختلفة للأرقام في دول العالم المختلفة ، نظرًا لأهمية الأرقام في الحياة اليومية وحياة الإنسان بشكل عام ، ومن هنا جاءت أهمية تقسيم الأرقام إلى مجموعات.

عدد المجموعات الرياضية

جاء تقسيم الأرقام إلى مجموعات لتسهيل العمليات الحسابية وفهم أوضح للمشكلات الرياضية. قسم علماء الرياضيات مجموعات الأرقام إلى المجموعات التالية

مجموعة الأرقام الإجمالية أو أرقام العد ، وهي المجموعة الأساسية والأساسية لمجموعات الأرقام ، وهي مجموعة الأرقام من 1 – 2 – 3 إلى ما لا نهاية ويرمز لها بالرمز (k).
مجموعة الأعداد الطبيعية ، وهي الأعداد التي تبدأ من الصفر بالإضافة إلى الأعداد الصحيحة ، مثل 0-1-2-3 إلى ما لا نهاية ويرمز لها بالرمز (i).
مجموعة الأعداد الصحيحة ، وهي الأعداد الطبيعية بالإضافة إلى الأعداد السالبة ، ويتم التعبير عنها بهذه الطريقة (ما لا نهاية …. 3- _ 2- _ 1- _ 0 _ 1 _ 2 _ 3 إلى ما لا نهاية) وهي يرمز لها بالرمز (y).
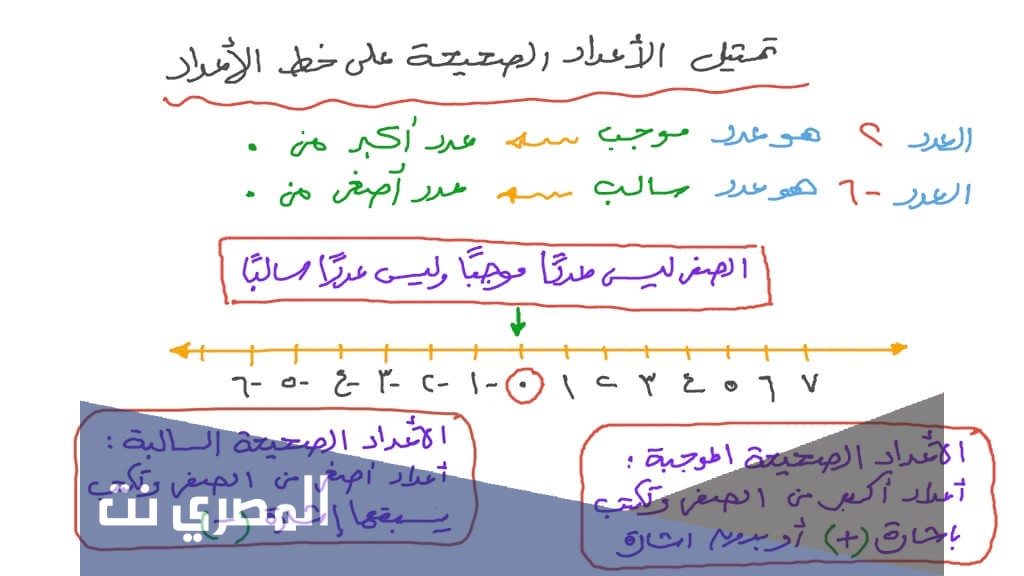
يمكن تقسيم مجموعة الأعداد الصحيحة إلى مجموعتين فرعيتين: مجموعة الأعداد الصحيحة السالبة (ما لا نهاية …. 3- _ 2- _ 1-) ومجموعة الأعداد الصحيحة الموجبة (1 – 2 – 3 إلى ما لا نهاية) ، حيث اتفق العلماء على أن الرقم صفر ليس رقمًا موجبًا أو سالبًا.
مجموعة الأعداد المنطقية والمُعبر عنها بالرمز (n) ، والذي يشير إلى جميع الأعداد الصحيحة التي يمكن التعبير عنها من خلال البسط والمقام ، بشرط ألا يكون المقام مساويًا للصفر ، وبالتالي يطلق عليها أيضًا مجموعة مختلطة الأرقام لأنه يتم التعبير عنها من خلال الكسور.
مجموعة الأرقام غير النسبية هي مجموعة الأرقام التي لا يمكن التعبير عنها في شكل كسور ، مثل الأرقام التي تقع تحت الجذر التربيعي ، مثل 2
مجموعة الأعداد الحقيقية هي مجموعة الأعداد المنطقية بالإضافة إلى مجموعة الأعداد غير المنطقية ، وهي جميع الأرقام التي يتم التعامل معها ، وهي أكثر مجموعة من الأرقام ويتم التعبير عنها بالرمز (ح).
مجموعة الأعداد الأولية ، وهي مجموعة خاصة تتضمن مجموعة الأعداد الطبيعية التي لا تقبل القسمة إلا على نفسها والرقم 1 ، مثل (1 – 3 – 5 – 7 – 11 – 13 – 17 إلى ما لا نهاية).
كل مجموعات الأرقام هي مجموعات لا نهائية.

ما هي الأعداد الصحيحة؟

الأعداد الصحيحة هي مجموعة الأرقام المستخدمة في العمليات الحسابية أو العد ، لذلك تسمى أيضًا مجموعة أرقام العد ، ويرمز إلى مجموعة الأعداد الصحيحة بالرمز (ك):

يمكن أيضًا تعريف الأعداد الصحيحة على أنها مجموعة الأعداد الطبيعية ناقص الصفر {k} = {i} – صفر.
مجموعة الأعداد الصحيحة هي أصغر مجموعة من الأعداد ، وهي مجموعة فرعية من مجموعة الأعداد الطبيعية ، ومجموعة الأعداد الطبيعية هي جزء من مجموعة الأعداد الصحيحة ، ومجموعة الأعداد الصحيحة هي جزء من مجموعة الأعداد الحقيقية .
مجموعة الأعداد الصحيحة هي 1،2،3،4 … إلى ما لا نهاية.
مجموعة الأعداد الصحيحة k = {1،2،3،4 ،… ..}
{k} {i} {r} {n} {h} حيث k هي مجموعة الأعداد الصحيحة ، i هي مجموعة الأعداد الطبيعية ، r هي مجموعة الأعداد الصحيحة ، n هي مجموعة الأعداد النسبية ، h هي مجموعة من الأعداد الحقيقية.

خصائص الأعداد الصحيحة

الأعداد الصحيحة هي 1،2،3 إلى ما لا نهاية ، وهي أرقام موجبة فقط ، ولا تتضمن الرقم صفر ، ولا تحتوي على أرقام سالبة أو كسرية أو عشرية:

العمليات على الأعداد الصحيحة: الضرب والقسمة والجمع والنتيجة هي دائمًا رقم موجب ينتمي إلى مجموعة الأعداد الصحيحة.
دائمًا ما يكون طرح الأعداد الصحيحة عددًا موجبًا في حالة واحدة ، وهو طرح الرقم من نفسه ، وبالتالي تكون النتيجة صفرًا ، والصفر ليس عددًا موجبًا أو سالبًا ولا ينتمي إلى مجموعة الأعداد الصحيحة.
لا يمكن تحت أي ظرف من الظروف أن تكون النتيجة قيمة سالبة أو رقم عشري أو كسر عند إجراء أي من العمليات الحسابية.
يمكن إجراء العمليات الحسابية من مجموعة أرقام العد مع أي مجموعة من مجموعات الأرقام الأخرى ، والنتيجة تنتمي إلى مجموعة الأرقام الأخرى وتنتمي إلى مجموعة الأعداد الصحيحة إذا كانت موجبة فقط ، وليست كسرية ، وليست عشرية ، ولا يساوي الصفر.

ما هي الأعداد الطبيعية

الأعداد الطبيعية هي مجموعة الأعداد الصحيحة الموجبة زائد الصفر ، وهي مجموعة من الأعداد اللانهائية، ويُشار إلى الأرقام الطبيعية بالرمز i في العمليات الحسابية باللغة العربية وبالرمز N في اللغة الإنجليزية ويشير الحرف N إلى الأعداد الطبيعية ، أي الأرقام الطبيعية في اللغة الإنجليزية:

مجموعة الأعداد الطبيعية هي i = {0،1،2،3،4} حيث يشير الرمز إلى اللانهاية.
من خصائص الأعداد الطبيعية الجبرية أن مجموعة الأعداد الطبيعية لها خاصية الإغلاق والتجميع والتبادل والتوزيع ، ويعتبر الصفر رقمًا محايدًا ، أي أنه ليس عددًا موجبًا أو سالبًا.
مجموعة الأعداد الطبيعية {y} هي مجموعة فرعية من مجموعة الأعداد الصحيحة {y} ، ومجموعة الأعداد الصحيحة هي مجموعة فرعية من مجموعة الأعداد المنطقية {n} ، ومجموعة الأعداد المنطقية هي مجموعة فرعية من مجموعة الأعداد الحقيقية {ح}.

ما لا تعرفه عن الأعداد الطبيعية

مجموعة الأعداد الطبيعية هي مجموعة الأعداد الصحيحة مطروحًا منها الأعداد السالبة ، أو بعبارة أخرى مجموعة الأعداد الطبيعية هي مجموعة الأعداد الصحيحة الموجبة زائد صفر:

{i} {r} {n} {h} حيث i هي مجموعة الأعداد الطبيعية ، و r هي مجموعة الأعداد الصحيحة ، و n هي مجموعة الأعداد النسبية ، و h هي مجموعة الأعداد الحقيقية.
مجموعة الأعداد الطبيعية هي 0،1،2،3 إلى ما لا نهاية ، ولا تحتوي على أي أرقام سالبة أو كسرية أو عشرية أو تحت الجذر.
العمليات على الأعداد الصحيحة ، الضرب ، القسمة ، الجمع والطرح ، ينتج عنها دائمًا رقم موجب ينتمي إلى مجموعة الأعداد الطبيعية ، وإذا كان حاصل الضرب صفرًا ، فهو ينتمي إلى مجموعة الأعداد الطبيعية ، لكنه رقم محايد ، أي أنه ليس رقمًا موجبًا أو سالبًا.
تحت أي ظرف من الظروف ، عند إجراء أي من العمليات الحسابية على مجموعة الأعداد الطبيعية ، يمكن أن تكون النتيجة قيمة سالبة أو عشري أو كسر.
يمكن إجراء العمليات الحسابية من مجموعة الأعداد الطبيعية مع أي مجموعة من مجموعات الأرقام الأخرى ، والنتيجة تنتمي إلى مجموعة الأرقام الأخرى وتنتمي إلى مجموعة الأعداد الطبيعية إذا كانت موجبة فقط وليست كسرًا ، وليس رقم عشري أو رقم سالب.

الأعداد الصحيحة هي واحدة من أصغر مجموعات الأرقام وهي التي يبدأ الأطفال في تعلمها ، لذلك من المهم معرفة ما هي الأعداد الصحيحة؟ لأنهم المجموعات التي يتعامل معها الأطفال ويعرفون قيمة وأهمية الأرقام في العمليات الحسابية والحياة العامة ونرجو الفائدة.