مساحة شبه المنحرف متساوي الساقين والقائم، شبه المنحرف هو شكل هندسي له 4 جوانب متتالية ، مع زوج واحد من الأضلاع المتوازية، شبه المنحرف هو شكل رباعي له زوج واحد من الأضلاع المتوازية وفي شبه منحرف تسمى الأضلاع المتوازية القواعد زوج من الزوايا التي تشترك في القاعدة كضلع مشترك يسمى زوج من الزوايا الأساسية، وشبه المنحرف مع جوانب غير متوازية من نفس الطول يسمى شبه منحرف متساوي الساقين، في هذا الموضوع سنوضح مساحة شبه المنحرف متساوي الساقين والقائم.
ما هو شبه منحرف؟
- شبه المنحرف هو شكل هندسي له 4 جوانب متتالية ، مع زوج واحد من الأضلاع المتوازية.
- شبه المنحرف هو شكل رباعي له زوج واحد من الأضلاع المتوازية ، وفي شبه منحرف تسمى الأضلاع المتوازية القواعد.
- زوج من الزوايا التي تشترك في القاعدة كضلع مشترك يسمى زوج من الزوايا الأساسية ، وشبه المنحرف مع جوانب غير متوازية من نفس الطول يسمى شبه منحرف متساوي الساقين ، وهذا التخمين يخبرنا أن الزوايا الأساسية هي متساوي الساقين شبه منحرف متساوي القياس.
- يمكن أن تكون الأضلاع المتوازية رأسية أو مائلة ، والمسافة العمودية بين الجوانب المتوازية تسمى الارتفاع.
- يمتد الجانبان العلوي والسفلي من شبه المنحرف بالتوازي مع بعضهما البعض ، لذا فهي قواعد شبه المنحرف ، وستتقاطع الجوانب الأخرى من شبه المنحرف إذا تم تمديدها ، بحيث تكون أرجل شبه المنحرف.
محيط شبه منحرف
تسمى الجوانب الأخرى من شبه المنحرف الموازية لبعضها البعض القواعد ، بينما تسمى الجوانب المتبقية من شبه المنحرف ، والتي تتقاطع عند نقطة ما إذا كانت ممتدة ، بأرجل شبه منحرف.
محيط شبه منحرف = مجموع أطوال أضلاعه.
محيط شبه المنحرف = طول القاعدة الرئيسية + طول القاعدة الثانوية + مجموع الأرجل.
منطقة شبه منحرف متساوي الساقين وشبه منحرف الأيمن
- يحدث شبه منحرف إذا كان كلا الزوجين من الضلعين المتقابلين متوازيين ؛ جميع جوانبها متساوية في الطول وزوايا قائمة مع بعضها البعض.
- إذا كان شبه المنحرف له زوايا قاعدية متطابقة ، فهو شبه منحرف متساوي الساقين ، فسنحقق في أقطار شبه منحرف متساوي الساقين.
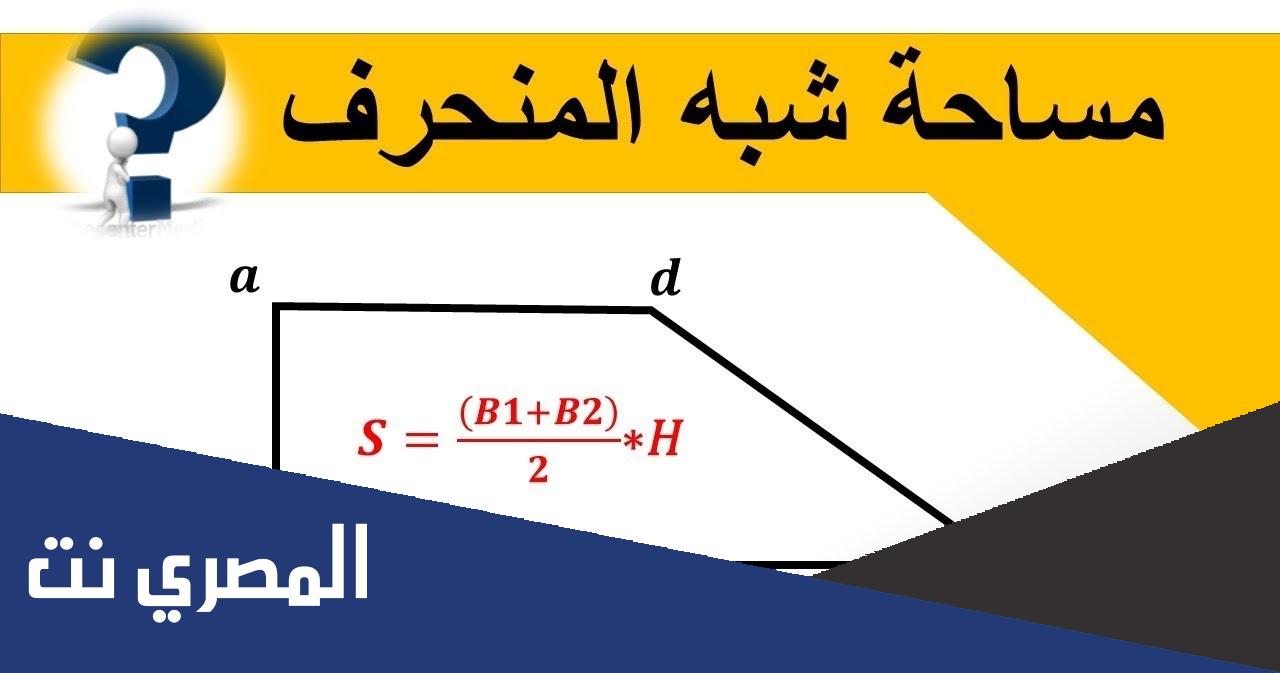
- مساحة شبه المنحرف = (مجموع القاعدتين / 2) × الارتفاع = ((طول القاعدة الرئيسية + طول القاعدة الصغرى) / 2) × الارتفاع
خصائص شبه منحرف
- شبه المنحرف هو شكل هندسي يكون فيه أزواج الأضلاع المتقابلة متوازية.
- مثلما تكون أقطار المستطيل متطابقة وتنقسم إلى بعضها البعض ، فإن أقطار شبه منحرف متساوي الساقين متطابقة أيضًا ، لكنها لا تنقسم.
- الجزء الأوسط (شبه منحرف) عبارة عن مقطع خطي يربط بين نقطتي المنتصف من الجانبين غير المتوازيين ، وهناك نقطة وسط واحدة فقط في شبه منحرف ، ستكون موازية للقواعد لأنها في منتصف المسافة بينهما.
- يمكن أن يكون الشكل شبه منحرف إذا كان كلا الزوجين من الضلعين المتقابلين متوازيين ؛ حيث الأضلاع المتقابلة متساوية في الطول وهناك زوايا قائمة لبعضها البعض.
- هناك بعض الأمثلة على شبه المنحرف في الحياة مثل وجه صندوق الفشار وحقيبة اليد والجسر.
حقائق ممتعة عن شبه المنحرف
- يُعرف شبه المنحرف باسم “pαπέζιο ‘p trapézion” في اليونانية القديمة والذي يعني حرفياً (طاولة صغيرة) ويشير أيضًا إلى “الرباعي غير المنتظم”.
- تم إدخال كلمة شبه منحرف في اللغة الإنجليزية في عام 1570 ، مع كون مارينوس بروكلوس أول شخص يستخدم كلمة شبه منحرف في الكتاب الأول من العناصر
- شبه المنحرف هو شكل مسطح له 4 جوانب مستقيمة لها زوج من الأضلاع المتوازية.
- تسمى الجوانب المتوازية “القواعد” ، بينما تسمى الجوانب الأخرى “الأرجل” (والتي قد تكون أو لا تكون متوازية).
- شبه منحرف متساوي الساقين هو شبه منحرف حيث يكون الجانبان غير المتوازيين متطابقين.
- محيط شبه المنحرف هو مجموع أطوال الأضلاع الأربعة. إذا كان أحد الأطوال أو أكثر غير معروف ، يمكنك أحيانًا استخدام نظرية فيثاغورس للعثور عليه.
- نظرًا لأن شبه المنحرف يجب أن يكون له زوج واحد من الأضلاع المتوازية تمامًا ، فسنحتاج إلى إثبات أن زوجًا من الأضلاع المتوازية متوازي والآخر ليس في البراهين الهندسية المكونة من عمودين.
- إذا نسينا إثبات أن زوجًا من الأضلاع المتقابلة ليسا متوازيين ، فإننا لا نستبعد احتمال أن يكون الرباعي متوازي أضلاع ، لذلك ستكون هذه الخطوة ضرورية للغاية عندما نعمل على تمارين مختلفة تتضمن شبه منحرف.
- سيكون من الضروري معرفة أسماء الأجزاء المختلفة من هذا الرباعي من أجل التحديد حول جوانبها وزواياها. تتكون كل شبه منحرف من جزأين رئيسيين: القواعد والأرجل.
إثبات أن شبه المنحرف هو شكل متساوي الساقين
هناك العديد من النظريات التي يمكننا استخدامها لمساعدتنا في إثبات أن شبه المنحرف هو متساوي الساقين. هذه الخصائص مذكورة أدناه:
شبه المنحرف هو متساوي الساقين إذا وفقط إذا كانت زوايا القاعدة متطابقة.
إذا كان شبه منحرف متساوي الساقين ، فإن الزاوية المقابلة لها تكون مكملة.
تصنيف شبه منحرف
- تُعطى المتوازيات ذات السمات الخاصة ، مثل الزوايا القائمة أو جميع الجوانب المتطابقة (أو كليهما) ، أسماء مميزة خاصة بها: المستطيل ، المعين ، والمربع.
- السمة الخاصة الوحيدة لشبه المنحرف التي تم إعطاؤها اسمها المميز هي الزوج الثاني من الجوانب المتوازية ، مما يجعل شبه المنحرف الخاص متوازي أضلاع.
- عندما تكون الأضلاع (بخلاف القواعد) من نفس الطول ، يُشار إلى شبه المنحرف باسم متساوي الساقين ، تمامًا كما تسمى المثلثات التي لها جانبان متساويان الطول (بخلاف القاعدة) مثلثات متساوية الساقين.
- لا توجد أسماء مميزة أخرى مستخدمة لشبه المنحرف بسمات خاصة (مثل الزوايا القائمة أو ثلاثة جوانب متطابقة).
- قد تكون الأضلاع المتوازية عمودية أو أفقية أو مائلة ، في الواقع من خلال التعريف ، يمكن القول إن الشكل شبه منحرف لأنه يحتوي على “زوج واحد على الأقل من الجوانب المتوازية” (ولا توجد ميزات أخرى مهمة).
- في بعض الأشكال ، يكون الجانبان الآخران متوازيين ، ولا يفيان أيضًا بمتطلبات شبه المنحرف (رباعي الأضلاع مع زوج واحد على الأقل من الجوانب المتوازية) ولكن أيضًا متطلبات كونه متوازي الأضلاع.
- التعريف أعلاه هو التعريف المقبول في مجتمع الرياضيات ، وبشكل متزايد في مجتمع التعليم ، العديد من المصادر المتعلقة بالتعليم من رياض الأطفال وحتى الصف الثاني عشر تقيد تاريخياً شبه المنحرف ليتطلب زوجًا واحدًا من الجوانب المتوازية تمامًا.
- يستثني هذا التعريف الأضيق متوازي الأضلاع كمجموعة فرعية من شبه المنحرف ، ولا يترك سوى الأشكال الأخرى. هذا التعريف الضيق يتعامل مع شبه المنحرفات كما لو كانت مثلثات مثل “قطع رأس واحدة موازية للجانب الآخر”.
الفرق بين شبه منحرف ومتوازي الأضلاع
- كما هو الحال مع أي شيء متعلق بالرياضيات ، نحتاج إلى تحسين سؤالنا ومعرفة ما نبحث عنه بالضبط.
- نريد هنا معرفة ما إذا كان شبه المنحرف متوازي أضلاع أم لا ، ويمكننا معرفة ذلك من خلال فهم ماهية متوازي الأضلاع بالضبط وما إذا كانت سمات هذا الشكل تتطابق مع متوازي الأضلاع.
- يُعرَّف متوازي الأضلاع بأنه رباعي الأضلاع (شكل له أربعة جوانب) وله زوجان من الأضلاع المتوازية.
- شبه المنحرف هو شكل رباعي له زوج واحد على الأقل من الأضلاع المتوازية ، في الواقع ، هذا لا يمكن أن يكون متوازي أضلاع ، لأنه يحتاج فقط إلى زوج واحد من الأضلاع المتوازية ، مما يعني أنه سيكون هناك شبه منحرف له زوج واحد فقط من الأضلاع المتوازية. الجوانب.
- يمتد هذا المنطق إلى جميع الألعاب الرياضية حيث تم إثبات خطأ العبارة إذا تمكنا من العثور على استثناء واحد على الأقل لـ “القاعدة”.
في ختام هذا الموضوع نكون قد تحدثنا عن مساحة شبه المنحرف متساوي الساقين والقائم، وتعرفنا علي اهم المعلومات التي تتعلق بتلك الموضوع، وتعرفنا علي شبه المنحرف ومحيط شبه المنحرف وخصائص شبه المنحرف، وتكلمنا عن حقائق ممتعة عن شبه المنحرف والفرق بين شبه المنحرف ومتوازي الاضلاع.